Математический курс «Комбинаторика»
Урок 6
Тема: сочетания без повторений
для 1-9 классов

Содержание урока
1. Видеоразбор задач
2. Объяснение темы на конкретных примерах
3. Математический лайфхак
4. Задачи для самостоятельного решения
2. Объяснение темы на конкретных примерах
3. Математический лайфхак
4. Задачи для самостоятельного решения
КОМБИНАТОРИКА — УРОК 6
Видеоразбор задач
Задача 1
Задача 2
На предыдущем уроке мы познакомились с понятием размещений (и перестановок, как частного случая размещений) и научились применять формулу для подсчёта перестановок. Теперь познакомимся с понятием сочетаний.
Сочетанием из n элементов по k называется набор содержащая k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми. Этим сочетания и отличаются от размещений – порядок следования элементов в выборке не важен.
Для подсчёта количества сочетаний без повторений (когда все элементы уникальны) используется формула:
Сочетанием из n элементов по k называется набор содержащая k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми. Этим сочетания и отличаются от размещений – порядок следования элементов в выборке не важен.
Для подсчёта количества сочетаний без повторений (когда все элементы уникальны) используется формула:
Условие
Боня пришла в магазин, чтобы купить красивые наборы столовых приборов для праздника. Но продавец сказал, что в последней привезенной партии среди 10 наборов три бракованных. Боня решила испытать удачу и купила три набора в надежде, что все они окажутся без брака. Сколькими способами она могла выбрать хотя бы один бракованный набор?
3
ПРИМЕР
Сочетания без повторений
Математический лайфхак
Как и в случае с использованием формулы для подсчёта перестановок, сперва нужно убедиться, что пользоваться формулой для решения конкретной задачи можно. Задай себе вопросы:
• Все ли элементы из доступных участвуют в сочетании? (Если да, то речь идёт о крайнем случае, используй правила!). Определи значения n и k.
• Учитывается ли порядок следования элементов? (Если да, то речь идёт о размещениях, формулу для их подсчёта мы изучили на прошлом уроке)
• Есть ли повторяющиеся элементы в множестве? (Если да, то формулой из этого урока пользоваться нельзя. Как быть в этой ситуации – рассмотрим в следующем уроке)
• Все ли элементы из доступных участвуют в сочетании? (Если да, то речь идёт о крайнем случае, используй правила!). Определи значения n и k.
• Учитывается ли порядок следования элементов? (Если да, то речь идёт о размещениях, формулу для их подсчёта мы изучили на прошлом уроке)
• Есть ли повторяющиеся элементы в множестве? (Если да, то формулой из этого урока пользоваться нельзя. Как быть в этой ситуации – рассмотрим в следующем уроке)
Условие
У Пифа есть 23 мячика, из которых 10 красных и 13 синих.
а) Сколькими способами можно выбрать два мячика одного цвета?
б) Сколькими способами можно выбрать два мячика разных цветов?
а) Сколькими способами можно выбрать два мячика одного цвета?
б) Сколькими способами можно выбрать два мячика разных цветов?
1
ПРИМЕР

где n – количество элементов в множестве, а k – количество «мест», доступных для размещения.
Лайфхак:
В формуле сочетаний существуют «крайние» значения. Их удобно запомнить, чтобы не выполнять лишних вычислений:
В формуле сочетаний существуют «крайние» значения. Их удобно запомнить, чтобы не выполнять лишних вычислений:

1) единственным способом можно не выбрать ни одного элемента
Условие
Пиф, Торик, Дед Пифагор и Боня хотят пойти куда-нибудь после обеда. Можно пойти на каток или в бассейн. Сколькими способами они могут распределиться между этими двумя занятиями? Каждый должен выбрать себе занятие, но, возможно, куда-то никто не придёт.
2
ПРИМЕР
2) n способами можно выбрать один элемент
3) n способами можно выбрать n-1 элемент (т.е. оставить один элемент)
4) единственным способом можно выбрать ВСЕ элементы
Давайте рассмотрим несколько примеров:
У Пифа есть 23 мячика, из которых 10 красных и 13 синих.
а) Сколькими способами можно выбрать два мячика одного цвета?
б) Сколькими способами можно выбрать два мячика разных цветов?
а) Сколькими способами можно выбрать два мячика одного цвета?
б) Сколькими способами можно выбрать два мячика разных цветов?
Для начала проанализируем, какие из известных правил мы должны использовать для решения этой задачи.
а) Пиф может выбрать 2 красных мячика ИЛИ 2 синих. В каком порядке он будет вытаскивать 2 шарика одного цвета – не важно. Значит мы можем использовать формулу для подсчёта числа сочетаний, а союз ИЛИ подразумевает применение правила суммы.
Найдём количество способов выбрать 2 красных мячика. Используем формулу сочетаний из десяти элементов по два (всего красных мячиков 10, k = 2, n = 10):
а) Пиф может выбрать 2 красных мячика ИЛИ 2 синих. В каком порядке он будет вытаскивать 2 шарика одного цвета – не важно. Значит мы можем использовать формулу для подсчёта числа сочетаний, а союз ИЛИ подразумевает применение правила суммы.
Найдём количество способов выбрать 2 красных мячика. Используем формулу сочетаний из десяти элементов по два (всего красных мячиков 10, k = 2, n = 10):
УСЛОВИЕ

РЕШЕНИЕ
Теперь найдём количество способов выбрать 2 синих мячика. Используем формулу сочетаний из тринадцати элементов по два (всего синих мячиков 13, k = 2, n = 13):

Поскольку выбор двух красных шариков исключает выбор двух синих и наоборот, используем правило суммы:
45 + 78 = 123 способа.
б) Пиф может выбрать один любой красный мячик из десяти и один любой синий шарик из тринадцати.
Количество способов выбрать красный мячик (k = 1, n = 10):
45 + 78 = 123 способа.
б) Пиф может выбрать один любой красный мячик из десяти и один любой синий шарик из тринадцати.
Количество способов выбрать красный мячик (k = 1, n = 10):
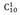
= 10 способов (крайний случай, десятью способами можно выбрать один элемент из десяти)
Количество способов выбрать синий мячик (k = 1, n = 13):
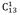
= 13 способов (крайний случай, тринадцатью способами можно выбрать один элемент из тринадцати)
Пиф выбирает один красный мячик И один синий. То есть каждый из выбранных красных мячиков может сочетаться с каждым из выбранных синих. Используем правило произведения для общего подсчёта количества способов такого выбора:
10 * 13 = 130 способов.
10 * 13 = 130 способов.
Пиф, Торик, Дед Пифагор и Боня хотят пойти куда-нибудь после обеда. Можно пойти на каток или в бассейн. Сколькими способами они могут распределиться между этими двумя занятиями? Каждый должен выбрать себе занятие, но, возможно, куда-то никто не придёт.
Подумаем, как могут распределиться наши герои.
1) Один может пойти на каток, а остальные – в бассейн.
2) Двое могут пойти на каток, а остальные – в бассейн.
3) Трое могут пойти на каток, а остальные – в бассейн.
4) Четверо могут пойти на каток, и никто – в бассейн.
И наоборот. То есть нам достаточно посчитать количество перечисленных способов выбора занятий, а потом умножить на два, тем самым поменяв героев местами – те кто ходил на каток теперь пойдут в бассейн, и наоборот
Рассмотрим первый случай:
1) Сколькими способами один герой может пойти на каток?
1) Один может пойти на каток, а остальные – в бассейн.
2) Двое могут пойти на каток, а остальные – в бассейн.
3) Трое могут пойти на каток, а остальные – в бассейн.
4) Четверо могут пойти на каток, и никто – в бассейн.
И наоборот. То есть нам достаточно посчитать количество перечисленных способов выбора занятий, а потом умножить на два, тем самым поменяв героев местами – те кто ходил на каток теперь пойдут в бассейн, и наоборот
Рассмотрим первый случай:
1) Сколькими способами один герой может пойти на каток?
УСЛОВИЕ
Сочетания без повторений обладают следующим свойством:
РЕШЕНИЕ

Давайте рассмотрим пример, для решения которого это может быть полезным:
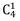
= 4 способа (крайний случай, четырьмя способами можно выбрать один элемент из четырёх)
А сколькими способами трое могут пойти на каток?

Способов получилось одинаковое количество. А это значит, что нам достаточно считать только количество способов отправить героев в какое-то одно место. Далее будем считать каток.
2) Сколькими способами двое могут пойти на каток?
2) Сколькими способами двое могут пойти на каток?

3) Сколькими способами трое могут пойти на каток?

4) Сколькими способами четверо могут пойти на каток?
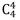
= 1 способ (крайний случай, единственным способом можно выбрать ВСЕ элементы из четырёх)
Поскольку между всеми перечисленными событиями можно поставить слово ИЛИ (один идёт на каток ИЛИ двое идут на каток ИЛИ трое…), используем правило суммы для подсчёта общего количества способов распределения:
4 + 6 + 4 + 1 = 15 способов.
А теперь поменяем героев местами. Например, в первом случае Торик ходил на каток один. А теперь он один пойдёт в бассейн. И так для всех героев:
15 * 2 = 30 способов.
4 + 6 + 4 + 1 = 15 способов.
А теперь поменяем героев местами. Например, в первом случае Торик ходил на каток один. А теперь он один пойдёт в бассейн. И так для всех героев:
15 * 2 = 30 способов.
Подсчитаем для начала, сколькими способами Боня могла выбрать три любых набора из десяти? k = 3, n = 10
УСЛОВИЕ
Боня пришла в магазин, чтобы купить красивые наборы столовых приборов для праздника. Но продавец сказал, что в последней привезенной партии среди 10 наборов три бракованных. Боня решила испытать удачу и купила три набора в надежде, что все они окажутся без брака. Сколькими способами она могла выбрать хотя бы один бракованный набор?
РЕШЕНИЕ

А теперь найдём число исходов, когда все три набора – без брака. Тогда в остальных случаях хотя бы один будет бракованным.
Выбирать теперь будем три набора ТОЛЬКО из наборов без брака. Если в наличии три бракованных набора из десяти. Тогда наборов без брака 10 – 3 = 7. Посчитаем количество сочетаний из семи по три:
Выбирать теперь будем три набора ТОЛЬКО из наборов без брака. Если в наличии три бракованных набора из десяти. Тогда наборов без брака 10 – 3 = 7. Посчитаем количество сочетаний из семи по три:

Теперь вычтем из общего количества способов выбрать три набора количество способов выбрать три набора без брака и получим количество способов выбрать три набора, среди которых хотя бы один бракованный:
120 – 35 = 85 способов.
120 – 35 = 85 способов.

Задачи для самостоятельного решения
Задача №1

Ниже ты найдёшь 5 задач для самостоятельного решения. Каждая задача помечена звёздочкой — это уровень сложности. Не спеши сразу смотреть решение с ответами. Постарайся самостоятельно разобраться в каждой задачке. У тебя всё получится! :)
Дедушка Пифагор собирает команду для игры «Что? Где? Когда?» из физиков и математиков. Сколькими способами можно собрать команду из 3 физиков и 4 математиков, если дед Пифагор знаком с 6 физиками и 8 математиками?
Пиф подбросил монету 9 раз. Сколько всего существует последовательностей, в которых «орёл» выпал ровно четыре раза?
Большой треугольник разбили на одинаковые части. Сколько способов закрасить ровно треть большого треугольника? Закрашивать кусочки, на которые он разбит, можно только целиком.
Торик строит замок из конструкторов двух наборов. Первую башенку он хочет построить из четырёх деталей первого набора, вторую – из шести деталей второго, а третью – из трёх любых деталей. Сколькими способами он может это сделать, если у него осталось 14 деталей: 6 из первого набора и 8 из второго?
Боня гуляет по аллее, вдоль которой рядами растут деревья. По правую сторону – 8 деревьев, а по левую — 11 деревьев. Боня захотела обвязать какие-то три дерева лентами, чтобы образовать их них треугольник. Сколькими способами она может это сделать?
Задача №3



Задача №5



Задача №4


Задача №2

Дедушка Пифагор собирает команду для игры «Что? Где? Когда?» из физиков и математиков. Сколькими способами можно собрать команду из 3 физиков и 4 математиков, если дед Пифагор знаком с 6 физиками и 8 математиками?
В команде у деда Пифагора должны быть и физики, и математики. Тогда найдём количество способов выбрать трёх любых физиков и четырёх любых математиков среди его знакомых, а затем, используя правило произведения (каждый из «наборов» физиков может сочетаться с каждым из «наборов» математиков), подсчитаем общее количество способов собрать команду для игры.
Количество способов выбрать трёх физиков из шести (количество сочетаний из шести элементов по три, n = 6, k = 3):
Количество способов выбрать трёх физиков из шести (количество сочетаний из шести элементов по три, n = 6, k = 3):

УСЛОВИЕ
РЕШЕНИЕ
Количество способов выбрать четырёх математиков из восьми (количество сочетаний из восьми элементов по четыре, n = 8, k = 4):

Количество комбинаций «наборов» физиков и математиков:
20 * 70 = 1400.
20 * 70 = 1400.
Пиф подбросил монету 9 раз. Сколько всего существует последовательностей, в которых «орёл» выпал ровно четыре раза?
Заметим, что последовательности будут отличаться только положением «орлов». Остальные позиции будут занимать «решки». Тогда нам достаточно посчитать количество способов выбрать четыре любых места из девяти имеющихся, на которых будет располагаться «орёл»:

Используя свойство сочетаний,
УСЛОВИЕ

РЕШЕНИЕ
точно такой же ответ мы получили бы, если бы положения выбирали не для «орлов», а для «решек». При четырёх выпавших «орлах» выпадет 9 – 4 = 5 «решек». Тогда количество способов выбрать пять любых мест из девяти имеющихся, на которых будет располагаться «решки»:

Большой треугольник разбили на одинаковые части. Сколько способов закрасить ровно треть большого треугольника? Закрашивать кусочки, на которые он разбит, можно только целиком.
Треугольник разбит на 9 одинаковых маленьких треугольничка. Чтобы закрасить ровно треть большого треугольника, нужно закрасить три любых маленьких треугольничка. Задача сводится к подсчёту количества сочетаний из девяти по три (k = 3, n = 9):
УСЛОВИЕ
РЕШЕНИЕ


Теперь количество способов выбрать детали из второго набора для второй башенки, то есть 6 деталей из восьми:
Для построения трёх башенок Торику понадобится 4 + 6 + 3 = 13 деталек.
Сначала подсчитаем количество способов выбрать детали из первого набора для первой башенки, то есть 4 детали из шести:
Сначала подсчитаем количество способов выбрать детали из первого набора для первой башенки, то есть 4 детали из шести:

УСЛОВИЕ
РЕШЕНИЕ
Торик строит замок из конструкторов двух наборов. Первую башенку он хочет построить из четырёх деталей первого набора, вторую – из шести деталей второго, а третью – из трёх любых деталей. Сколькими способами он может это сделать, если у него осталось 14 деталей: 6 из первого набора и 8 из второго?

Осталось 2 детали из первого набора и 2 детали из второго набора. Осталось выбрать из них три детали для недостающей башенки. Это можно сделать двумя способами:
1) Выбрать 2 детали из первого набора и одну из второго.
Выбираем одну деталь из второго набора, остальные будут из первого:
1) Выбрать 2 детали из первого набора и одну из второго.
Выбираем одну деталь из второго набора, остальные будут из первого:
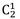
= 2 способа ("крайний" случай, 2 способа выбрать одну деталь из двух)
2) Выбрать две детали из второго набора и одну из первого.
Выбираем одну деталь из первого набора, остальные будут из второго:
Выбираем одну деталь из первого набора, остальные будут из второго:
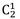
= 2 способа ("крайний" случай, 2 способа выбрать одну деталь из двух)
Итого, нам нужно собрать первую башенку из деталей первого набора И вторую из деталей второго набора И третью башенку из двух возможных случаев (2 детали из второго набора и одна из первого ИЛИ две детали из первого набора и одна из второго).
Количество способов построить третью башенку находим по правилу суммы:
2 + 2 = 4 способа.
Каждый из способов построить первую башенку может сочетаться с каждым из способов построить вторую башенку и с каждым из способов построить третью башенку. По правилу произведения находим количество способов построить все три башенки:
15 * 28 * 4 = 1680 способов
Количество способов построить третью башенку находим по правилу суммы:
2 + 2 = 4 способа.
Каждый из способов построить первую башенку может сочетаться с каждым из способов построить вторую башенку и с каждым из способов построить третью башенку. По правилу произведения находим количество способов построить все три башенки:
15 * 28 * 4 = 1680 способов
Боня гуляет по аллее, вдоль которой рядами растут деревья. По правую сторону – 8 деревьев, а по левую — 11 деревьев. Боня захотела обвязать какие-то три дерева лентами, чтобы образовать их них треугольник. Сколькими способами она может это сделать?
Рассмотрим, как Боня может выбрать три дерева, образующих треугольник:
1) Одно дерево по правую сторону от аллеи и два – по левую.
2) Одно дерево по левую сторону от аллеи и два – по правую.
В первом случае по правую сторону можно выбрать одно дерево из восьми, т.е. k = 1, n = 8. Это «крайний» случай:
1) Одно дерево по правую сторону от аллеи и два – по левую.
2) Одно дерево по левую сторону от аллеи и два – по правую.
В первом случае по правую сторону можно выбрать одно дерево из восьми, т.е. k = 1, n = 8. Это «крайний» случай:
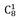
= 8 способов выбрать дерево по правую сторону от аллеи.
УСЛОВИЕ
А по левую сторону она может выбрать два дерева из одиннадцати, т.е. k = 2, n = 11:
РЕШЕНИЕ

Итого 55 способов выбрать 2 дерева по левую сторону от аллеи.
Каждое из выбранных по правую сторону от аллеи деревьев можно сочетать с каждой из пар выбранных по левую сторону деревьев. Используем правило умножения:
8 * 55 = 440 способов выбрать три дерева в первом случае.
Во втором случае по левую сторону можно выбрать одно дерево из одиннадцати, т.е. k = 1, n = 11. Это «крайний» случай:
Каждое из выбранных по правую сторону от аллеи деревьев можно сочетать с каждой из пар выбранных по левую сторону деревьев. Используем правило умножения:
8 * 55 = 440 способов выбрать три дерева в первом случае.
Во втором случае по левую сторону можно выбрать одно дерево из одиннадцати, т.е. k = 1, n = 11. Это «крайний» случай:
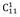
= 11 способов выбрать дерево по левую сторону от аллеи.
Теперь по правую сторону она может выбрать два дерева из восьми, т.е. k = 2, n = 8:

Итого 28 способов выбрать 2 дерева по правую сторону от аллеи.
Каждое из выбранных по левую сторону от аллеи деревьев можно сочетать с каждой из пар выбранных по правую сторону деревьев. Используем правило умножения:
11 * 28 = 308 способов выбрать три дерева во втором случае.
Боня может выбрать деревья по первому принципу ИЛИ по второму. Для подсчёта общего числа возможных треугольников используем правило суммы:
440 + 308 = 748 способов.
Каждое из выбранных по левую сторону от аллеи деревьев можно сочетать с каждой из пар выбранных по правую сторону деревьев. Используем правило умножения:
11 * 28 = 308 способов выбрать три дерева во втором случае.
Боня может выбрать деревья по первому принципу ИЛИ по второму. Для подсчёта общего числа возможных треугольников используем правило суммы:
440 + 308 = 748 способов.
При возникновении вопросов можете связаться с нами:
E-mail: pifshtany@gmail.com
WhatsApp: +7 905 743 04 39
E-mail: pifshtany@gmail.com
WhatsApp: +7 905 743 04 39
Политика в отношении обработки персональных данных
1. Общие положения
Настоящая политика обработки персональных данных составлена в соответствии с требованиями Федерального закона от 27.07.2006. №152-ФЗ «О персональных данных» и определяет порядок обработки персональных данных и меры по обеспечению безопасности персональных данных, предпринимаемые Жуковой Анастасией Андреевной (далее – Оператор).
1.1. Оператор ставит своей важнейшей целью и условием осуществления своей деятельности соблюдение прав и свобод человека и гражданина при обработке его персональных данных, в том числе защиты прав на неприкосновенность частной жизни, личную и семейную тайну.
1.2. Настоящая политика Оператора в отношении обработки персональных данных (далее – Политика) применяется ко всей информации, которую Оператор может получить о посетителях веб-сайта http://pifshtany.ru/.
2. Основные понятия, используемые в Политике
2.1. Автоматизированная обработка персональных данных – обработка персональных данных с помощью средств вычислительной техники;
2.2. Блокирование персональных данных – временное прекращение обработки персональных данных (за исключением случаев, если обработка необходима для уточнения персональных данных);
2.3. Веб-сайт – совокупность графических и информационных материалов, а также программ для ЭВМ и баз данных, обеспечивающих их доступность в сети интернет по сетевому адресу http://pifshtany.ru/;
2.4. Информационная система персональных данных — совокупность содержащихся в базах данных персональных данных, и обеспечивающих их обработку информационных технологий и технических средств;
2.5. Обезличивание персональных данных — действия, в результате которых невозможно определить без использования дополнительной информации принадлежность персональных данных конкретному Пользователю или иному субъекту персональных данных;
2.6. Обработка персональных данных – любое действие (операция) или совокупность действий (операций), совершаемых с использованием средств автоматизации или без использования таких средств с персональными данными, включая сбор, запись, систематизацию, накопление, хранение, уточнение (обновление, изменение), извлечение, использование, передачу (распространение, предоставление, доступ), обезличивание, блокирование, удаление, уничтожение персональных данных;
2.7. Оператор – государственный орган, муниципальный орган, юридическое или физическое лицо, самостоятельно или совместно с другими лицами организующие и (или) осуществляющие обработку персональных данных, а также определяющие цели обработки персональных данных, состав персональных данных, подлежащих обработке, действия (операции), совершаемые с персональными данными;
2.8. Персональные данные – любая информация, относящаяся прямо или косвенно к определенному или определяемому Пользователю веб-сайта http://pifshtany.ru/;
2.9. Пользователь – любой посетитель веб-сайта http://pifshtany.ru/;
2.10. Предоставление персональных данных – действия, направленные на раскрытие персональных данных определенному лицу или определенному кругу лиц;
2.11. Распространение персональных данных – любые действия, направленные на раскрытие персональных данных неопределенному кругу лиц (передача персональных данных) или на ознакомление с персональными данными неограниченного круга лиц, в том числе обнародование персональных данных в средствах массовой информации, размещение в информационно-телекоммуникационных сетях или предоставление доступа к персональным данным каким-либо иным способом;
2.12. Трансграничная передача персональных данных – передача персональных данных на территорию иностранного государства органу власти иностранного государства, иностранному физическому или иностранному юридическому лицу;
2.13. Уничтожение персональных данных – любые действия, в результате которых персональные данные уничтожаются безвозвратно с невозможностью дальнейшего восстановления содержания персональных данных в информационной системе персональных данных и (или) уничтожаются материальные носители персональных данных.
3. Оператор может обрабатывать следующие персональные данные Пользователя
3.1. Фамилия, имя, отчество;
3.2. Электронный адрес;
3.3. Номера телефонов;
3.4. Год, месяц, дата и место рождения;
3.5. Также на сайте происходит сбор и обработка обезличенных данных о посетителях (в т.ч. файлов «cookie») с помощью сервисов интернет-статистики (Яндекс Метрика и Гугл Аналитика и других).
3.6. Вышеперечисленные данные далее по тексту Политики объединены общим понятием Персональные данные.
4. Цели обработки персональных данных
4.1. Цель обработки персональных данных Пользователя — информирование Пользователя посредством отправки электронных писем; заключение, исполнение и прекращение гражданско-правовых договоров; предоставление доступа Пользователю к сервисам, информации и/или материалам, содержащимся на веб-сайте.
4.2. Также Оператор имеет право направлять Пользователю уведомления о новых продуктах и услугах, специальных предложениях и различных событиях. Пользователь всегда может отказаться от получения информационных сообщений, направив Оператору письмо на адрес электронной почты an.an.zhukova@gmail.com с пометкой «Отказ от уведомлений о новых продуктах и услугах и специальных предложениях».
4.3. Обезличенные данные Пользователей, собираемые с помощью сервисов интернет-статистики, служат для сбора информации о действиях Пользователей на сайте, улучшения качества сайта и его содержания.
5. Правовые основания обработки персональных данных
5.1. Оператор обрабатывает персональные данные Пользователя только в случае их заполнения и/или отправки Пользователем самостоятельно через специальные формы, расположенные на сайте http://pifshtany.ru/. Заполняя соответствующие формы и/или отправляя свои персональные данные Оператору, Пользователь выражает свое согласие с данной Политикой.
5.2. Оператор обрабатывает обезличенные данные о Пользователе в случае, если это разрешено в настройках браузера Пользователя (включено сохранение файлов «cookie» и использованиетехнологии JavaScript).
6. Порядок сбора, хранения, передачи и других видов обработки персональных данных
Безопасность персональных данных, которые обрабатываются Оператором, обеспечивается путем реализации правовых, организационных и технических мер, необходимых для выполнения в полном объеме требований действующего законодательства в области защиты персональных данных.
6.1. Оператор обеспечивает сохранность персональных данных и принимает все возможные меры, исключающие доступ к персональным данным неуполномоченных лиц.
6.2. Персональные данные Пользователя никогда, ни при каких условиях не будут переданы третьим лицам, за исключением случаев, связанных с исполнением действующего законодательства.
6.3. В случае выявления неточностей в персональных данных, Пользователь может актуализировать их самостоятельно, путем направления Оператору уведомление на адрес электронной почты Оператора an.an.zhukova@gmail.com с пометкой «Актуализация персональных данных».
6.4. Срок обработки персональных данных является неограниченным. Пользователь может в любой момент отозвать свое согласие на обработку персональных данных, направив Оператору уведомление посредством электронной почты на электронный адрес Оператора an.an.zhukova@gmail.com с пометкой «Отзыв согласия на обработку персональных данных».
7. Трансграничная передача персональных данных
7.1. Оператор до начала осуществления трансграничной передачи персональных данных обязан убедиться в том, что иностранным государством, на территорию которого предполагается осуществлять передачу персональных данных, обеспечивается надежная защита прав субъектов персональных данных.
7.2. Трансграничная передача персональных данных на территории иностранных государств, не отвечающих вышеуказанным требованиям, может осуществляться только в случае наличия согласия в письменной форме субъекта персональных данных на трансграничную передачу его персональных данных и/или исполнения договора, стороной которого является субъект персональных данных.
8. Заключительные положения
8.1. Пользователь может получить любые разъяснения по интересующим вопросам, касающимся обработки его персональных данных, обратившись к Оператору с помощью электронной почты an.an.zhukova@gmail.com.
8.2. В данном документе будут отражены любые изменения политики обработки персональных данных Оператором. Политика действует бессрочно до замены ее новой версией.
8.3. Актуальная версия Политики в свободном доступе расположена в сети Интернет по адресу http://pifshtany.ru/.
Настоящая политика обработки персональных данных составлена в соответствии с требованиями Федерального закона от 27.07.2006. №152-ФЗ «О персональных данных» и определяет порядок обработки персональных данных и меры по обеспечению безопасности персональных данных, предпринимаемые Жуковой Анастасией Андреевной (далее – Оператор).
1.1. Оператор ставит своей важнейшей целью и условием осуществления своей деятельности соблюдение прав и свобод человека и гражданина при обработке его персональных данных, в том числе защиты прав на неприкосновенность частной жизни, личную и семейную тайну.
1.2. Настоящая политика Оператора в отношении обработки персональных данных (далее – Политика) применяется ко всей информации, которую Оператор может получить о посетителях веб-сайта http://pifshtany.ru/.
2. Основные понятия, используемые в Политике
2.1. Автоматизированная обработка персональных данных – обработка персональных данных с помощью средств вычислительной техники;
2.2. Блокирование персональных данных – временное прекращение обработки персональных данных (за исключением случаев, если обработка необходима для уточнения персональных данных);
2.3. Веб-сайт – совокупность графических и информационных материалов, а также программ для ЭВМ и баз данных, обеспечивающих их доступность в сети интернет по сетевому адресу http://pifshtany.ru/;
2.4. Информационная система персональных данных — совокупность содержащихся в базах данных персональных данных, и обеспечивающих их обработку информационных технологий и технических средств;
2.5. Обезличивание персональных данных — действия, в результате которых невозможно определить без использования дополнительной информации принадлежность персональных данных конкретному Пользователю или иному субъекту персональных данных;
2.6. Обработка персональных данных – любое действие (операция) или совокупность действий (операций), совершаемых с использованием средств автоматизации или без использования таких средств с персональными данными, включая сбор, запись, систематизацию, накопление, хранение, уточнение (обновление, изменение), извлечение, использование, передачу (распространение, предоставление, доступ), обезличивание, блокирование, удаление, уничтожение персональных данных;
2.7. Оператор – государственный орган, муниципальный орган, юридическое или физическое лицо, самостоятельно или совместно с другими лицами организующие и (или) осуществляющие обработку персональных данных, а также определяющие цели обработки персональных данных, состав персональных данных, подлежащих обработке, действия (операции), совершаемые с персональными данными;
2.8. Персональные данные – любая информация, относящаяся прямо или косвенно к определенному или определяемому Пользователю веб-сайта http://pifshtany.ru/;
2.9. Пользователь – любой посетитель веб-сайта http://pifshtany.ru/;
2.10. Предоставление персональных данных – действия, направленные на раскрытие персональных данных определенному лицу или определенному кругу лиц;
2.11. Распространение персональных данных – любые действия, направленные на раскрытие персональных данных неопределенному кругу лиц (передача персональных данных) или на ознакомление с персональными данными неограниченного круга лиц, в том числе обнародование персональных данных в средствах массовой информации, размещение в информационно-телекоммуникационных сетях или предоставление доступа к персональным данным каким-либо иным способом;
2.12. Трансграничная передача персональных данных – передача персональных данных на территорию иностранного государства органу власти иностранного государства, иностранному физическому или иностранному юридическому лицу;
2.13. Уничтожение персональных данных – любые действия, в результате которых персональные данные уничтожаются безвозвратно с невозможностью дальнейшего восстановления содержания персональных данных в информационной системе персональных данных и (или) уничтожаются материальные носители персональных данных.
3. Оператор может обрабатывать следующие персональные данные Пользователя
3.1. Фамилия, имя, отчество;
3.2. Электронный адрес;
3.3. Номера телефонов;
3.4. Год, месяц, дата и место рождения;
3.5. Также на сайте происходит сбор и обработка обезличенных данных о посетителях (в т.ч. файлов «cookie») с помощью сервисов интернет-статистики (Яндекс Метрика и Гугл Аналитика и других).
3.6. Вышеперечисленные данные далее по тексту Политики объединены общим понятием Персональные данные.
4. Цели обработки персональных данных
4.1. Цель обработки персональных данных Пользователя — информирование Пользователя посредством отправки электронных писем; заключение, исполнение и прекращение гражданско-правовых договоров; предоставление доступа Пользователю к сервисам, информации и/или материалам, содержащимся на веб-сайте.
4.2. Также Оператор имеет право направлять Пользователю уведомления о новых продуктах и услугах, специальных предложениях и различных событиях. Пользователь всегда может отказаться от получения информационных сообщений, направив Оператору письмо на адрес электронной почты an.an.zhukova@gmail.com с пометкой «Отказ от уведомлений о новых продуктах и услугах и специальных предложениях».
4.3. Обезличенные данные Пользователей, собираемые с помощью сервисов интернет-статистики, служат для сбора информации о действиях Пользователей на сайте, улучшения качества сайта и его содержания.
5. Правовые основания обработки персональных данных
5.1. Оператор обрабатывает персональные данные Пользователя только в случае их заполнения и/или отправки Пользователем самостоятельно через специальные формы, расположенные на сайте http://pifshtany.ru/. Заполняя соответствующие формы и/или отправляя свои персональные данные Оператору, Пользователь выражает свое согласие с данной Политикой.
5.2. Оператор обрабатывает обезличенные данные о Пользователе в случае, если это разрешено в настройках браузера Пользователя (включено сохранение файлов «cookie» и использованиетехнологии JavaScript).
6. Порядок сбора, хранения, передачи и других видов обработки персональных данных
Безопасность персональных данных, которые обрабатываются Оператором, обеспечивается путем реализации правовых, организационных и технических мер, необходимых для выполнения в полном объеме требований действующего законодательства в области защиты персональных данных.
6.1. Оператор обеспечивает сохранность персональных данных и принимает все возможные меры, исключающие доступ к персональным данным неуполномоченных лиц.
6.2. Персональные данные Пользователя никогда, ни при каких условиях не будут переданы третьим лицам, за исключением случаев, связанных с исполнением действующего законодательства.
6.3. В случае выявления неточностей в персональных данных, Пользователь может актуализировать их самостоятельно, путем направления Оператору уведомление на адрес электронной почты Оператора an.an.zhukova@gmail.com с пометкой «Актуализация персональных данных».
6.4. Срок обработки персональных данных является неограниченным. Пользователь может в любой момент отозвать свое согласие на обработку персональных данных, направив Оператору уведомление посредством электронной почты на электронный адрес Оператора an.an.zhukova@gmail.com с пометкой «Отзыв согласия на обработку персональных данных».
7. Трансграничная передача персональных данных
7.1. Оператор до начала осуществления трансграничной передачи персональных данных обязан убедиться в том, что иностранным государством, на территорию которого предполагается осуществлять передачу персональных данных, обеспечивается надежная защита прав субъектов персональных данных.
7.2. Трансграничная передача персональных данных на территории иностранных государств, не отвечающих вышеуказанным требованиям, может осуществляться только в случае наличия согласия в письменной форме субъекта персональных данных на трансграничную передачу его персональных данных и/или исполнения договора, стороной которого является субъект персональных данных.
8. Заключительные положения
8.1. Пользователь может получить любые разъяснения по интересующим вопросам, касающимся обработки его персональных данных, обратившись к Оператору с помощью электронной почты an.an.zhukova@gmail.com.
8.2. В данном документе будут отражены любые изменения политики обработки персональных данных Оператором. Политика действует бессрочно до замены ее новой версией.
8.3. Актуальная версия Политики в свободном доступе расположена в сети Интернет по адресу http://pifshtany.ru/.
