Математический курс «Комбинаторика»
Урок 4
Сайт курса
Тема: факториал и перестановки
для 1-9 классов
Содержание урока
1. Видеоразбор задач

2. Объяснение темы на конкретных примерах

3. Математический лайфхак

4. Задачи для самостоятельного решения
Математический интенсив
«Подготовка к поступлению в маткласс»
Интенсивная подготовка к предстоящим вступительным в матклассы, где вместе с преподавателями Мехмата МГУ будут разобраны и прорешены основные задачи
для 4-6 классов
Сайт интенсива
27 и 28 января
ОНЛАЙН
КОМБИНАТОРИКА — УРОК 4
Видеоразбор задач
Задача 1
Задача 2
В предыдущих уроках мы уже рассматривали некоторые задачи на перестановки и использовали правило умножения для их решения (Пример 1). Теперь, когда мы разобрались с тем, что такое перестановки, рассмотрим задачи, в которых можно использовать формулу для их нахождения (Пример 2, 3)
Факториал и перестановки
Условие
У Пифа есть 5 кубиков разных цветов: жёлтый, зелёный, синий, оранжевый и розовый. Сколькими способами он может выстроить пирамидку из 5 кубиков?
ОТКРЫТЬ РЕШЕНИЕ
1
ПРИМЕР
Условие
У Бони есть 6 карточек с цифрами 0, 3, 4, 5, 7 и 9. Она составляет из них шестизначные числа. Сколько различных чисел у неё может получиться?
ОТКРЫТЬ РЕШЕНИЕ
2
ПРИМЕР
Условие
Торик собрал из кубиков своё имя, а затем начал переставлять кубики, но непременно так, чтобы буквы Т, О и Р стояли рядом. Сколько слов может собрать Торик, следуя такому правилу?
ОТКРЫТЬ РЕШЕНИЕ
3
ПРИМЕР
Математический лайфхак
Неспроста мы начали с решения задач с использованием правила произведения, ведь для того, чтобы его применить, необходимо произвести анализ каждой позиции. Бездумное использование формулы для перестановок может привести к подсчету лишних вариантов, и задача будет решена неверно. Поэтому перед тем, как подставлять числа в формулу, необходимо задаться вопросом: «А есть ли какие-то исключения?»
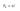
У Пифа есть 5 кубиков разных цветов: жёлтый, зелёный, синий, оранжевый и розовый. Сколькими способами он может выстроить пирамидку из 5 кубиков?
На прошлых уроках мы рассуждали следующим образом:

Первым кубиком Пиф может поставить один кубик из пяти (любого цвета), вторым – один из четырёх (любой, кроме того, который ин уже использовал), третьим – один из трёх, четвёртым – один из двух, пятым – последний оставшийся. То есть существует 5 способов выбрать первый кубик, 4 способа выбрать второй, 3 способа выбрать третий, 2 способа выбрать четвёртый и 1 способ выбрать пятый кубик.

Тогда, используя правило произведения, мы находили количество различных пирамидок, которые Пиф может составить: 5 х 4 х 3 х 2 х 1 = 120.

В математике существует особая форма записи для такого произведения. Мы могли записать это произведение как 5! (читается «пять-факториал»).

Факториал числа — это произведение натуральных чисел от 1 до этого числа (включая это число). Факториал обозначается восклицательным знаком после числа.

По сути, мы находили количество возможных ПЕРЕСТАНОВОК цветов. Например, жёлтый кубик может стоять на первом месте, а может на втором, а может на третьем, четвертом или пятом. То же самое с остальными цветами.

Размещение n элементов множества БЕЗ ПОВТОРЕНИЙ, то есть, когда все размещаемые элементы уникальны (встречаются только один раз), называется перестановкой из n элементов. Количество перестановок принято обозначать буквой P. И найти его можно, используя формулу:

УСЛОВИЕ
РЕШЕНИЕ
где n – количество размещаемых элементов (в нашем примере n = 5, имеется 5 РАЗНЫХ цветов)
Теперь, когда мы разобрались с тем, что такое перестановки, рассмотрим задачи, в которых можно использовать формулу для их нахождения:
У Бони есть 6 карточек с цифрами 0, 3, 4, 5, 7 и 9. Она составляет из них шестизначные числа. Сколько различных чисел у неё может получиться?
В предыдущих уроках мы решали подобные задачи, используя правило произведения - на первом месте в числе может стоять любая цифра, кроме 0, то есть существует 5 вариантов выбора первой цифры, на втором месте может стоять любая цифра (включая 0), кроме уже использованной, то есть существует пять вариантов выбора второй цифры, на третьем месте может стоять любая цифра из четырёх оставшихся, на четвертом – любая из трёх оставшихся, на пятом – из двух, на шестом – последняя оставшаяся. Тогда чисел можно составить 5 * 5 * 4 * 3 * 2 * 1 = 600.

Эту же задачу можно решить, используя формулу для нахождения перестановок, но так как 0 не может стоять на первом месте, то полученные числа, начинающиеся с нуля необходимо исключить. То есть:

1) Считаем, сколько всего перестановок можно получить из 6 цифр:
2) Если на первом месте стоит ноль (он фиксирован), то перестановки происходят только среди пяти последующих чисел. И количество «чисел», начинающихся с нуля, будет равно количеству этих перестановок:
Осталось лишь вычесть из количества перестановок из шести цифр перестановки, которые нам не подходят (начинаются с нуля): 720 – 120 = 600.
УСЛОВИЕ
РЕШЕНИЕ
Торик собрал из кубиков своё имя, а затем начал переставлять кубики, но непременно так, чтобы буквы Т, О и Р стояли рядом. Сколько слов может собрать Торик, следуя такому правилу?
В имени Торика 5 букв. Чтобы три буквы Т, О и Р стояли рядом, первая из этих букв (не важно, какая именно), может быть расположена на первом, втором или третьем месте.
УСЛОВИЕ
РЕШЕНИЕ
А теперь разберемся с порядком расположения букв. Каждая из букв Т, О и Р может быть расположена на одном из трёх рядом расположенных мест. Количество перестановок этих трёх букв:
Но буквы И и К тоже могут располагаться в разном порядке. Рассмотрим теперь количество перестановок букв И, К и (какого-нибудь слова из букв Т, О, Р) – то есть снова перестановок трёх элементов:
И в каждой из этих перестановок мы можем сделать по 6 перестановок букв Т, О и Р. Значит общее количество возможных слов: 6 * 6 = 36.
Задачи для самостоятельного решения
Ниже ты найдёшь 5 задач для самостоятельного решения. Каждая задача помечена звёздочкой — это уровень сложности. Не спеши сразу смотреть решение с ответами. Постарайся самостоятельно разобраться в каждой задачке. У тебя всё получится! :)
На каждом из пяти ярусов новогодней ёлки располагается одна из гирлянд: с дождиком, с зайчиками, с белочками, со звездой и с ангелом. Сколькими способами можно нарядить ёлку, если верхний ярус обязательно должны украшать звезда или ангел?
Открыть решение
Пиф коллекционирует фантики, и Торик подарил ему 7 новых экспонатов для коллекции – два разных фантика от конфет «Ромашка», три разных фантика от конфет «Красная шапочка», фантик от конфеты «Гусиные лапки» и фантик от конфеты «Алёнка». Сколькими различными способами Пиф может разместить фантики на странице своего альбома?
Открыть решение
Боня выкладывает в ряд бусины из 4 треугольных и 3 круглых разноцветных бусин. Сколькими способами она может составить ряд, используя все бусины, если круглые и треугольные должны чередоваться?
Открыть решение
Дед Пифагор наводит порядок в своей библиотеке. На одной из полок у него стоит 10 книг, 4 из которых – учебники (по математике, философии, физике и астрономии), а остальные – различные журналы. Сколькими способами дед Пифагор может расставить книги на полке, чтобы учебники стояли рядом?
Открыть решение
У Торика есть 9 различных игрушек и 3 различных ящика. Сколькими способами он может разложить игрушки по ящикам так, чтобы в первом ящике оказалось 4 игрушки, во втором – три, а в третьем – две?
Открыть решение
Задача №1
Задача №5
Задача №3
Задача №4
Задача №2
На каждом из пяти ярусов новогодней ёлки располагается одна из гирлянд: с дождиком, с зайчиками, с белочками, со звездой и с ангелом. Сколькими способами можно нарядить ёлку, если верхний ярус обязательно должны украшать звезда или ангел?
Для начала «зафиксируем» на верхнем ярусе гирлянду со звездой и посчитаем количество возможных перестановок четырёх оставшихся гирлянд на четырёх оставшихся ярусах:
УСЛОВИЕ
РЕШЕНИЕ
Если верхний ярус украшает звезда, то существует 24 способа нарядить ёлку. Если же расположить на верхнем ярусе ангела, количество перестановок будет рассчитываться аналогично, и также равно 24. Поскольку эти способы украшения не могут сочетаться между собой (на верхушке звезда ИЛИ ангел), для подсчёта общего количества способов нарядить ёлку используем правило суммы: 24 + 24 = 48.
Пиф коллекционирует фантики, и Торик подари ему 7 новых экспонатов для коллекции – два разных фантика от конфет «Ромашка», три разных фантика от конфет «Красная шапочка», фантик от конфеты «Гусиные лапки» и фантик от конфеты «Алёнка». Сколькими различными способами Пиф может разместить фантики на странице своего альбома?
Т.к. на самом деле все объекты разные и даже фантики одного типа различны, то решение выглядит как обычный факториал:
УСЛОВИЕ
РЕШЕНИЕ
Боня выкладывает в ряд бусины из 4 треугольных и 3 круглых разноцветных бусин. Сколькими способами она может составить ряд, используя все бусины, если круглые и квадратные должны чередоваться?
Чтобы выполнилось условие чередования бусин, они должны располагаться в таком порядке:

Т К Т К Т К Т

То есть треугольные бусины могут быть расположены только на нечётных местах, а круглые – на чётных. И менять местами треугольные бусины можно только с треугольными, а круглые – с круглыми. Четыре треугольных бусины можно расположить на четырёх нечётных местах. Количество перестановок треугольных бусин будет равно:
УСЛОВИЕ
РЕШЕНИЕ
Три круглых бусины могут быть расположены на трёх чётных местах. Количество перестановок круглых бусин будет равно:
Каждый способ размещения квадратных бусин может сочетаться с каждым способом размещения треугольных бусин, значит, для подсчёта общего количества способов составить бусы, используем правило произведения: 6 * 24 = 144.
Дед Пифагор наводит порядок в своей библиотеке. На одной из полок у него стоит 10 книг, 4 из которых – учебники (по математике, философии, физике и астрономии), а остальные – различные журналы. Сколькими способами дед Пифагор может расставить книги на полке, чтобы учебники стояли рядом?
Рассмотрим ситуации, когда 4 учебника могут стоять рядом (пока не важно, в каком порядке):
УСЛОВИЕ
РЕШЕНИЕ
Видно, что первый из учебников может стоять на любом месте с 1 по 7.

А теперь определимся с порядком размещения учебников. Все четыре учебника РАЗНЫЕ и каждый из них может стоять по порядку первым, вторым, третьим или четвертым. Тогда рассчитаем количество перестановок этих учебников:
То есть если учебники занимают на полке места с 1 по 4, то существует 24 способа размещения учебников. И если учебники занимают на полке места со 2 по 5, то также существует 24 способа размещения учебников. И так до ситуации, когда первый учебник стоит на полке седьмым, а четвертый, соответственно, десятым.

А теперь рассмотрим расстановку шести журналов. Они тоже могут располагаться в разном порядке. Теперь подсчитаем количество перестановок шести журналов и какого-нибудь сочетания учебников – то есть перестановок семи элементов.
И в каждой из этих перестановок мы можем сделать по 24 перестановки четырёх учебников. Значит общее количество возможных расстановок книг на полке: 5040 * 24 = 120960.
У Торика есть 9 различных игрушек и 3 различных ящика. Сколькими способами он может разложить игрушки по ящикам так, чтобы в первом ящике оказалось 4 игрушки, во втором – три, а в третьем – две?
Представим, что игрушки не разложены по ящикам, а выложены в ряд. Тогда количество перестановок девяти разных игрушек можем рассчитать по формуле:
УСЛОВИЕ
РЕШЕНИЕ
Игрушки, лежащие в ящике, не упорядочены, то есть нам нужно исключить те перестановки, которые получены «различным размещением» игрушек внутри одного ящика.

В первом ящике помещается 4 игрушки, нам не важно в каком порядке. Количество перестановок этих четырех игрушек:
Во втором ящике помещается 3 игрушки. Количество перестановок этих трёх игрушек:
И наконец, в третьем ящике помещается 2 игрушки. Количество перестановок двух игрушек:
Осталось лишь исключить эти перестановки из числа перестановок девяти игрушек:
Переходи в чат курса, чтобы задать вопросы!
website icon
Чат курса
При возникновении вопросов можете связаться с нами:
E-mail: pifshtany@gmail.com
WhatsApp: +7 905 743 04 39