Математический курс «Комбинаторика»
Урок 1
Сайт курса
Тема: перебор вариантов
для 1-9 классов
Содержание урока
1. Видеоразбор задач

2. Объяснение темы на конкретных примерах

3. Математический лайфхак

4. Задачи для самостоятельного решения
КОМБИНАТОРИКА — УРОК 1
Видеоразбор задач
Задача 1
Задача 2
В комбинаторике мы будем постоянно считать количество способов что-нибудь сделать. Например, сколько способов доехать из Москвы в Екатеринбург или сколько существует вариантов подарка из трех разных книг? Задач будет много, c разными условиями и вопросами.

Cейчас мы познакомимся с самым базовым методом комбинаторики, который можно применять для решения любой из задач. Этот метод мы называем перебор вариантов. А суть его очень проста — перечислить все возможные варианты и посчитать их количество. Но даже простейший перебор надо делать с умом, чтобы выиграть время и ничего не упустить. Приступим!

Рассмотрим способы перебора на следующих 3-х примерах:
Перебор вариантов
Условие
Маша, Петя, Вася, Женя и Толя играют в салки. Ребята договорились, что каждый будет водящим один раз, и решили провести жеребьёвку, чтобы определиться, в каком порядке они будут водить. Сколько существует вариантов распределения жребия?
ОТКРЫТЬ РЕШЕНИЕ
3
ПРИМЕР
Математический лайфхак

В задачах на перебор легко допустить ошибку, пропустив какой-то из вариантов. Чтобы этого не произошло, не пиши все приходящие в голову варианты вразброс! Используй один из перечисленных нами методов для наглядности и структуры. Тогда и задачка быстрее решится, и ошибок по невнимательности не будет.

Условие
У Люси есть 3 разных вагончика: синий, красный и жёлтый. Сколькими способами она может составить паровозик из трёх вагончиков?
ОТКРЫТЬ РЕШЕНИЕ
1
ПРИМЕР
Условие
У собачки Бони 4 разных игрушки и три домика. Сколькими способами она может расположить игрушки в домике, если ни один домик не должен остаться пустым и в домике может лежать только одна игрушка?
ОТКРЫТЬ РЕШЕНИЕ
2
ПРИМЕР
У Люси есть 3 разных вагончика: синий, красный и жёлтый. Сколькими способами она может составить паровозик из трёх вагончиков?
Выберем какой-то один вагончик (например, жёлтый), и поставим его первым.
УСЛОВИЕ
Тогда вторым может быть красный вагончик, а третьим – синий:
А ещё вторым может быть синий вагончик, а третьим – красный:
Так мы перебрали все способы размещения вагончиков, при условии, что первый – жёлтый. Их два.
А теперь выберем другой вагончик (например, красный) и поставим его на первое место:
В этом случае вторым может стать синий вагончик, тогда третьим – желтый:
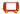
И наоборот: вторым станет жёлтый вагончик, тогда третьим – синий:
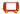
При размещении на первом месте красного вагончика также получаем два варианта поезда.
Нетрудно догадаться, что при размещении на первом месте синего вагончика вариантов тоже будет два:
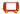
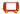
Всего получилось 2 + 2 + 2 = 6 вариантов раскраски поезда! Значит, Люся может составить поезд из трёх вагончиков шестью способами.
Теперь, когда мы изобразили все варианты поезда, давайте сделаем вывод! Можно было перебрать количество способов для одного вагончика (например, желтого) на первом месте, а затем умножить полученное число на все количество вагончиков, которые мы можем поставить на первое место

2 способа x 3 (жёлтый, красный, синий) = 6 способов.

Также в задачах иногда просят перечислить возможные варианты, что теперь не составит труда сделать:

желтый – красный – синий, жёлтый – синий – красный,

красный – синий – желтый, красный – жёлтый – синий,

синий – жёлтый – красный, синий – красный – жёлтый.

Эту задачу можно решить при помощи умножения. У нас есть три «места» для вагончиков. На первое место три варианта поставить вагон – жёлтый, красный или синий. Тогда на второе место остается два варианта (так как один мы уже использовали на первом месте). А на третье место остается только один вариант - последний оставшийся вагончик.
Получается: 3 x 2 x 1 = 6 способов!

Этот метод мы подробно разберем в следующих уроках
ЛАЙФХАК
РЕШЕНИЕ
Рассмотрим более сложную задачу, в которой в одном способе не используются все возможные опции выбора. То есть количество позиций размещения меньше количества возможных опций.

Вот пример такой задачи:
У собачки Бони 4 разных игрушки и три домика. Сколькими способами она может расположить игрушки в домике, если ни один домик не должен остаться пустым и в домике может лежать только одна игрушка?
Каждый из домиков – это «позиция», на которой может быть размещена одна из четырёх игрушек. Обозначим игрушки буквами А, Б, В, Г и переберем все возможные варианты их группировки для начала для первых двух домиков.

А Б
А В
А Г
Б А
Б В
Б Г
В А
В Б
В Г
Г А
Г Б
Г В






Получилось 12 вариантов. Осталось каждый из перечисленных вариантов дополнить третьей игрушкой.
Для АБ - это будет итогово АБВ и АБГ
Для АВ - АВБ и АВГ
Заметим, что каждый из перечисленных превратится в 2 варианта. Сложим 12 раз по 2 (или умножим) и получим ответ: 24 варианта

УСЛОВИЕ
РЕШЕНИЕ
Если объектов мало, перебор нагляден. Но даже на 5 объектах уже просто запутаться. В таких случаях на помощь приходит «дерево вариантов».

Разберем этот инструмент на примере задачи ниже
Маша, Петя, Вася, Женя и Толя играют в салки. Ребята договорились, что каждый будет водящим один раз, и решили провести жеребьёвку, чтобы определиться, в каком порядке они будут водить. Сколько существует вариантов распределения жребия?
Для решения этой задачи удобно использовать первые буквы имён ребят: Маша – М, Петя – П, Вася – В, Женя – Ж, Толя – Т.
Выберем первого водящего. Пусть это будет Маша. Она станет «основанием» нашего дерева. А от неё пойдут веточки к ребятам, которые по результату жребия могут стать вторыми:
Теперь от каждого второго водящего пройдут веточки к возможным третьим:
УСЛОВИЕ
Далее от каждого третьего к возможным четвёртым:
И, наконец, к оставшимся – пятым:
Подсчитаем количество веточек, образовавшихся внизу получившегося дерева – их 24. А поскольку в «основание» дерева можно поставить любого из пяти ребят, всего способов распределения жребия будет 24 х 5 = 120.
РЕШЕНИЕ
Задачи для самостоятельного решения:
Ниже ты найдёшь 5 задач для самостоятельного решения. Каждая задача помечена звёздочкой — это уровень сложности. Не спеши сразу смотреть решение с ответами. Постарайся самостоятельно разобраться в каждой задачке. У тебя всё получится! :)
Пифу подарили сундучок с двухзначным кодовым замочком для секретиков. На каждую из двух позиций кода можно поставить одну их 4 букв: П, И, Ф, У. Повторять буквы нельзя. Сколькими способами Пиф может придумать код для своего сундучка?
Задача №1
Открыть решение
Торик, Пиф, дедушка Пифагор и Боня записываются в список для участия в математическом турнире. Сколькими способами их можно расположить в списке?
Открыть решение
У дедушки Пифагора есть 6 книжек: красная, синяя, желтая, черная, белая и зелёная. Он хочет расставить их в ряд на полке. Сколькими способами он может это сделать?
Задача №2
Задача №3
Открыть решение
У Торика есть 7 карточек с цифрами от 1 до 7. Он выкладывает три карточки в ряд, чтобы образовалось трёхзначное число. Сколько чисел сможет выложить Торик?
Открыть решение
У Пифа есть 11 разных марок. Он хочет вклеить их в свой альбом. Но на странице помещается только шесть марок, а оставшиеся, в процессе вклеивания, Пиф по одной дарит Торику. Сколько различных комбинаций марок может получить в подарок Торик?
(Порядок выдачи Торику марок учитывается)
Задача №5
Открыть решение
Задача №4
Пифу подарили сундучок с двухзначным кодовым замочком для секретиков. На каждую из двух позиций кода можно поставить одну их 4 букв: П, И, Ф, У. Сколькими способами Пиф может придумать код для своего сундучка?
УСЛОВИЕ
Для начала переберем все возможные комбинации, когда на первом месте кода стоит буква П: П И, П Ф, П У – таких три. Если на первое место поставить любую из трёх оставшихся букв – И, Ф, У – с каждой будет так же три комбинации. Всего способов выбрать первую букву четыре. Получается: 4 х 3 = 12 способов.
РЕШЕНИЕ
Торик, Пиф, дедушка Пифагор и Боня записываются в список для участия в математическом турнире. Сколькими способами их можно расположить в списке?
Для начала, рассмотрим случаи, когда первым в списке участников окажется дедушка Пифагор.

Построим дерево вариантов:
УСЛОВИЕ
Получилось 6 способов такого расположения в списке.

Но первым так же может быть и Торик, и Пиф, и Боня, то есть первого в списке можно выбрать четырьмя способами, и с каждым первым можно составить 6 комбинаций.

Получается 4 x 6 = 24 способа.

РЕШЕНИЕ
У дедушки Пифагора есть 6 книжек: красная, синяя, желтая, черная, белая и зелёная. Он хочет расставить их в ряд на полке. Сколькими способами он может это сделать?
Первой на полку дедушка Пифагор может поставить одну из шести книжек, которые у него есть. Тогда второй - любую из пяти (кроме той, которую он уже поставил), третьей – любую из четырех оставшихся, четвертой – любую из трёх, пятой – любую из двух, шестой – последнюю (одну). Найдём количество способов расположения книжек:

6 x 5 x 4 x 3 x 2 x 1 = 720 способов.

УСЛОВИЕ
РЕШЕНИЕ
У Торика есть 7 карточек с цифрами от 1 до 7. Он выкладывает три карточки в ряд, чтобы образовалось трёхзначное число. Сколько чисел сможет выложить Торик?
Пусть первой Торик выложил карточку с цифрой 1. Посмотрим, сколько трехзначных чисел, начинающихся с единицы, он сможет составить:

УСЛОВИЕ
Таких чисел оказалось 30. Но первой может быть выложена любая из семи карточек, и начиная с каждой можно составить 30 трехзначных чисел.
Тогда общее количество чисел, которые могут получиться:
7 x 30 = 210.
РЕШЕНИЕ
Другой способ:
Первой Торик может выложить любую из семи карточек, второй – любую из шести (кроме той, которую он выложит первой), третьей – любую из пяти оставшихся. Тогда количество возможных комбинаций можно рассчитать как 7 х 6 х 5 = 210.
1 2 3
1 2 4
1 2 5
1 2 6
1 2 7
1 3 2
1 3 4
1 3 5
1 3 6
1 3 7
1 4 2
1 4 3
1 4 5
1 4 6
1 4 7
1 5 2
1 5 3
1 5 4
1 5 6
1 5 7
1 6 2
1 6 3
1 6 4
1 6 5
1 6 7
1 7 2
1 7 3
1 7 4
1 7 5
1 7 6
У Пифа есть 11 разных марок. Он хочет вклеить их в свой альбом. Но на странице помещается только шесть марок, а оставшиеся, в процессе вклеивания, Пиф по одной дарит Торику. Сколько различных комбинаций марок может получить в подарок Торик?
(Порядок выдачи Торику марок учитывается)
В этой задаче нам нужно рассмотреть именно комбинации марок, которые может получить Торик. Понятно, что ему достанутся те марки, которые Пиф не вклеит в свой альбом, а вклеит Пиф любые 6 марок, значит любые 5 (которые останутся) – Торик получит в подарок. Первой может попасться любая их 11 марок, второй – любая из 10, третьей – любая из 9, четвёртой – любая из 8, пятой – любая из 7.

Тогда количество возможных комбинаций из пяти марок найдём как: 11 х 10 х 9 х 8 х 7 = 55440.

УСЛОВИЕ
РЕШЕНИЕ
Переходи в чат курса, чтобы задать вопросы!
website icon
Чат курса
При возникновении вопросов можете связаться с нами:
E-mail: pifshtany@gmail.com
WhatsApp: +7 905 743 04 39